문제
[원문 링크]
그래프가 주어졌을 때, 단절선을 모두 구해 출력하는 프로그램을 작성하시오.
단절선이란 그 간선을 제거했을 때, 그래프가 두 개 또는 그 이상으로 나누어지는 간선을 말한다. 즉, 제거했을 때 그래프의 connected component의 개수가 증가하는 간선을 말한다.
입력
첫째 줄에 두 정수 V(1≤V≤100,000), E(1≤E≤1,000,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정수 A, B가 주어진다. 이는 A번 정점과 B번 정점이 연결되어 있다는 의미이며, 방향은 양방향이다.
그래프는 항상 연결되어 있으며, 같은 간선이 두 번 이상 들어오는 경우는 없다. 또, A와 B가 같은 경우도 없다.
그래프의 정점은 1부터 V까지 자연수이다.
출력
첫째 줄에 단절선의 개수 K를 출력한다.
둘째 줄부터 K개 줄에는 단절선을 사전순으로 한 줄에 하나씩 출력한다. 간선은 “A B” 형식으로 출력해야 하고, A < B를 만족해야 한다. 같은 간선은 한 번만 출력하면 된다. 즉, “A B”를 출력한 경우에 “B A”는 출력할 필요가 없다.
해설
그래프의 단절선을 찾는 문제이다. 단절선이란, 그래프에서 간선 하나를 지웠을 때 그래프가 둘로 나뉘게 되는 간선을 말한다.
단절선을 찾으려면, 주어진 그래프를 DFS로 돌면서 부모 정점, 방문 순서를 기록해두고, 다시 방문 순서 역순으로 정점을 돌면서 자신의 방문 순서가 부모 정점를 제외한 정점들의 방문 순서와 비교해 가장 이르면, 자신과 부모정점를 잇는 간선을 단절선으로 지정하고, 만약 다른 정덤 더 이르다면, 자신의 방문 순서를 그 정점의 방문순서로 갱신시켜주는 방식으로 구해줄 수 있다.
한 문장으로 이해하기는 어려운 개념이므로 그림으로 설명하려고 한다. 먼저 아래 그림을 보자.
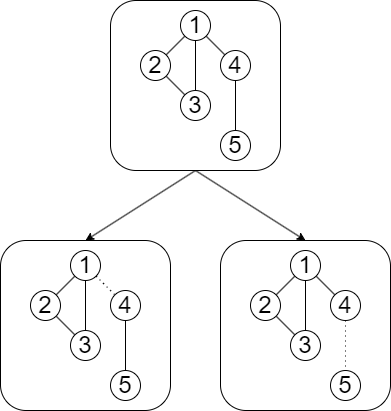
위와 같은 그래프가 주어졌을 때:
- 간선 (1, 4)를 지우면, 그래프가 [1, 2, 3]과 [4, 5]로 나뉘고,
- 간선 (4, 5)를 지우면, 그래프가 [1, 2, 3, 4]와 [5]로 나뉜다.
따라서 구해주어야 하는 단절선은 (1, 4)와 (4, 5)이다.
먼저 1번 정점을 시작으로 DFS를 돌려주면, 아래와 같은 그림이 된다.
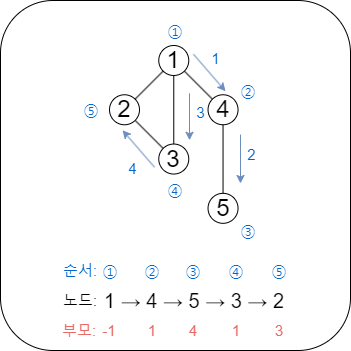
위 그림은 높은 번호의 정점을 가장 먼저 탐색했을 때 나오는 방문 순서이다. 각 정점의 부모 정점은 해당 정점까지 도달하기 위해 방문한 바로 이전 정점이다. 1번 정점은 부모 정점이 없기 때문에, -1로 설정되었다.
위 그림에서도 보면 알 수 있지만, 단절선으로 지정 가능한 간선들은 (ex. (1, 4)), 둘 중 자식 정점에 해당하는 것의 방문 순서가 (ex. 4번 정점의 방문 순서 ②), 부모 정점을 제외한 다른 정점들보다 이르다(ex. 1번 정점을 제외한 5번 정점의 방문 순서 ③보다 이르다)는 것을 알 수 있다.
하지만 단절선이 아닌 간선 중에서도 주위 정점의 방문 순서가 이른 경우(ex. (2, 3)의 경우, 1번 정점이 방문 순서 ①)도 있다. 이런 경우를 걸러내기 위해서 방문 순서를 역으로 돌면서 방문 순서를 갱신시켜주는 방법을 사용해야 한다. 아래의 그림을 보자.
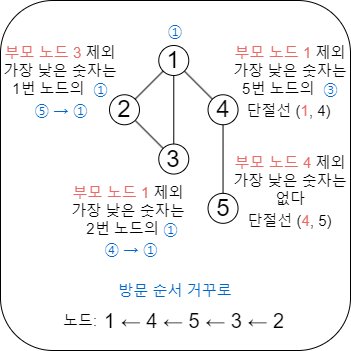
위 그래프에서 방문 순서 갱신 처리는 다음과 같은 순서로 진행된다:
- 2번 정점 방문순서 = ②, 부모 정점 3번을 제외한 정점들 중 가장 이른 방문 순서 = 1번 정점의 ①
- 2번 정점의 방문 순서를 ①로 갱신
- 3번 정점 방문순서 = ④, 부모 정점 1번을 제외한 정점들 중 가장 이른 방문 순서 = 2번 정점의 ①
- 3번 정점의 방문 순서를 ①로 갱신
- 5번 정점 방문순서 = ③, 부모 정점 4번을 제외한 정점들 중 가장 이른 방문 순서 = 없음
- (4, 5)는 단절선
- 4번 정점 방문순서 = ②, 부모 정점 1번을 제외한 정점들 중 가장 이른 방문 순서 = 5번 정점의 ③
- (1, 4)는 단절선
- 1번 정점과 이어지는 간선들은 이미 모두 탐색되었으므로, 생략 가능
이렇게 구해진 단절선 (1, 4) 와 (4, 5)를 반환하는 것이 단절선 구하는 알고리즘이다.
코드
위의 방법 그대로 구현한 코드이다.
파이썬은 재귀적으로 그래프를 탐색하면 while문으로 탐색하는 것보다 느려지기 때문에, 해당 코드에서는 while문을 사용하는 DFS를 적용했다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
import sys
input = sys.stdin.readline
def main():
V, E = map(int, input().split())
V += 1
graph = [[] for _ in range(V)]
visit = [0] * V # 방문 안했으면 0을, 방문 했으면 부모 노드를 기록
order = [0] * V # 방문 순서를 기록
count = [] # 방문한 노드 순서대로 저장
for _ in range(E):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
# DFS 돌면서 방문 순서, 부모노드 기록
queue = [(1, -1)]
while queue:
curr, prev = queue.pop()
if visit[curr]:
continue
visit[curr] = prev
count.append(curr)
order[curr] = len(count)
for next in graph[curr]:
if not visit[next]:
queue.append((next, curr))
# 방문 순서 역순으로 탐색하며 순서 갱신 및 단절선 탐색
result = []
for curr in count[:0:-1]:
is_bridge = True
for next in graph[curr]:
if next == visit[curr]:
continue
if order[curr] > order[next]:
is_bridge = False
order[curr] = order[next]
if is_bridge:
result.append(sorted([curr, visit[curr]]))
# 단절선을 사전순으로 정렬해 출력
result.sort()
answer = [str(len(result))]
answer.append('\n'.join(' '.join(map(str, k)) for k in result))
return '\n'.join(answer)
if __name__ == "__main__":
print(main())
